Control in Times of Crisis 2020 -- 2021.
Online seminar.
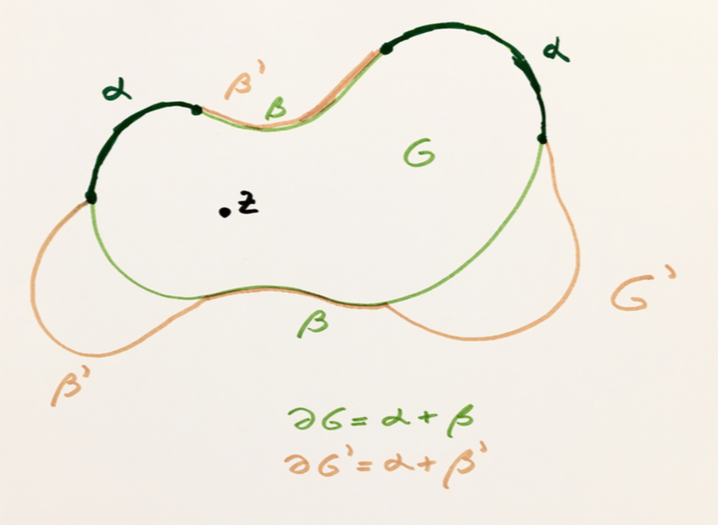




This scientific activity is a continuation of the online seminar Control en Tiempos de Crisis, this time addressing the international community interested in mathematical problems from control of differential equations, inverse problems and related subjects.
The seminar took each thursday at 10 AM in Mexico / 11:00 AM in Chile / 12:00 PM in Brasilia / 5:00 PM in Berlin, Roma, Madrid, Paris in the platform Zoom, alternating talks of senior and junior researchers.
All talks are available on our youtube channel. Talks:| Date | Speaker | Title / Abstract |
|---|---|---|
| September 8 | Jean-Michel Coron (U Pierre et Marie Curie, France) |
Rapid and finite-time stabilization.
We present various results on the rapid and the finite-time stabilization of control systems. This includes control systems in finite dimension (with an application to a quadcopter sliding on a plane) as well as control systems modeled by means of partial differential equations (1-D linear hyperbolic systems, 1-D linear parabolic equations and KdV equations). Slides. youtube link |
| September 15 Talk 1 |
Claudia Moreno (Université Paris-Saclay (UVSQ)) |
Control of a partial differential equation system of dispersive type.
In this talk, we study the exact controllability of a system composed by N Korteweg-de Vries equations. This model is known in the litera- ture as the KdV equation on a finite star-shaped network which is used to model for instance the cardiovascular system. The system originally was controlled in the literature considering N Korteweg-de Vries equations and N + 1 controls : N controls at the ends of the network and one control in the center of the network. We prove that the system remains controllable without the control acting in the center of the network. Thus, we prove the exact controllability of the system with N controls. We use the duality and multiplier method to study the controllability of the linearized system around the origin and the result for the nonlinear system is obtained by applying a fixed-point argument. Slides. youtube link |
| September 15 Talk 2 |
Irene Marin-Gayte (U Sevilla, Spain) |
Theoretical and numerical bi-objective optimal control: Nash equilibria.
This talk deals with the solution of some multi-objective optimal control problems for several PDEs: linear and semilinear elliptic equations and stationary Navier-Stokes systems. More precisely, we look for Nash equilibria associated to standard cost functionals. We deduce appropiate optimality sys- -tems and we present some iterative algorithms. For the existence and characterization of Nash equilibria in the Navier-Stokes case, we use the formalism of Dubovitskii and Milyutin. In this framework, we also present a finite element approximation of the bi-objective problem and we illustrate the techniques with several numerical experiments. Slides. youtube link |
| September 22 | Marius Tucsnak (U Bordeaux, France) |
Does the boundary controlled heat equation define an exactly controllable system?
It is commonly accepted in the control theory of PDEs that parabolic equations, due to the smoothing effect, do not determine exactly controllable systems when controlled from the boundary. The aim of this presentation is to explain how the heat semigroup can be restricted to an appropriate function space on which, when controlled from the boundary, it could determine an exactly controllable systems. To this aim, we first recall some abstract concepts concerning reachability in an infinite dimensional context, insisting on the general relevance of the concept of reachable space. We next describe some recent advances on the reachable space of the boundary controlled heat equation in one space dimension. We next discuss the exact controllability of this system in appropriate spaces of analytic functions. We give applications in determining the reachable space with smooth inputs, with possible application to nonlinear problems. Finally, we discuss the possible implications of our methods to improve the existing estimates of the control constant in small time. Slides. youtube link |
| September 29 Talk 1 |
José Antonio Villa (UNAM, Mexico) |
Hierarchical control for the semilinear heat equation.
Abstract: We present some results about hierarchical control of the semilinear heat equation where the follower control must steer the solution to zero in some positive time and the leader control must minimise a given functional. Also, results about the same objectives control problem are done for the case when the controls are both inner controls and boundary conditions. Slides. youtube link |
| September 29 Talk 2 |
Gilcenio Rodrigues (U F di Piaui, Brazil) |
Boundary controllability of a one-dimensional phase-field system with one control force
Abstract. Slides. youtube link |
| October 6 | Piermarco Cannarsa (U Roma 2, Italy) |
Bilinear control for evolution equations
Abstract: Bilinear control systems are receiving increasing attention as they can be used to study problems for which an additive control action is out of question. For such systems, in infinite dimension, weaker controllability properties can be expected than for additive controls. For instance, exact controllability is out of question due to a well-known negative result by Ball, Marsden, and Slemrod back in the 80ies. Nevertheless, one can seek to steer states to special targets either in finite or infinite time.In this talk, the above problem will be addressed for evolution equations of the form u'(t)=Au(t)+p(t)Bu(t) where A and B are linear operators in a Hilbert space and p(t) is a single-input control. Applications to parabolic equations in one space dimension will also be discussed. Slides. youtube link |
| October 13 Talk 1 |
Amaury Hayat (Ecole des Ponts Paristech) |
Stabilization of some nonlinear hyperbolic PDEs
Abstract: We consider two types of systems : density-velocity systems and traffic flows. Density-velocity systems encompass many physical equations: isentropic Euler equations, Saint-Venant equations, osmosis model, etc. We show that these equations have a local dissipative property that allows to stabilize any steady-state with boundary feedback controls, provided some physical assumption. Moreover, this holds even if we have no knowledge of some the system parameters or with a single control. Traffic flows are very interesting from a control perspective. In many situations the steady-states are unstable, leading to travelling waves, known as stop-and-go waves by engineers or simply jam. From a mathematical point of view they can be represented by coupled hyperbolic PDEs with solutions of class BV. We will present on-going work showing how one can try to stabilize the steady-states using autonomous vehicles, i.e. pointwise controls. This leads to a system of ODEs and PDEs coupled by a flux relation, which provoke non-classical shocks. The solutions are then at most BV and the control is contained in the dynamics of the ODEs. youtube link |
| October 13 Talk 2 |
Chenmin Sun (U. Cergy) |
Classical and semi-classical observability for the Bouendi-Grushin operator
Abstract: The observability for the classical Schrödinger equation usually holds for very short time, under suitable geometric conditions. However, it is not the case when the underlying geometry is sub-elliptic. In this talk we consider the Schrodinger equation associated with the Bouendi- Grushin operator. The Bouendi-Grushin operator is a subelliptic operator which is degenerate along a line. In the Bouendi case, the associated Schrödinger equation exhibits a transport effect which leads to a "sub-elliptic" geometric control condition and a minimal time to ensure the observability. For general Bouendi-Grushin with stronger sub-elliptic effect, the observability for the Schrödinger equation is never true. These observability results can be seen from a semi- classical point of view, through a optimal resolvent esti- mate. Consequently, our resolvent estimate leads to an energy decay rate for the associated damped wave equation. This talk is based on a joint work with Nicolas Burq and another with Cyril Letrouit. Slides. youtube link |
| October 20 | Karl Kunisch (U Graz, Austria) |
Solution Concepts for Optimal Feedback Control of Nonlinear Partial Differential Equations
Abstract: Feedback control of nonlinear systems in practice is still frequently based on linearisation and subsequent treatment by efficient Riccati solvers. Here we want to follow different directions. I concentrate on three solution strategies which aim at the nonlinear control system directly. The first one is based on higher order Taylor expansions of the value function and leads to controls which rely on generalized Ljapunov equations. The second approach is based on Newton steps applied to the HJB equation. Combined with spectral techniques and tensor calculus this allows to solve HJB equations up to dimension 100. The results are demonstrated for the control of discretized Fokker Planck equations. The third technique circumvents the direct solution of the HJB equation. Rather a neural network is trained by means of a succinctly chosen ansatz and it is proven that it approximates the solution to the HJB equation as the dimension of the network is increased. This work relies on collaborations with T.Breiten, S.Dolgov, D.Kalise, L.Pfeiffer, and D.Walter. Slides. youtube link |
| October 27 Talk 1 |
Yuri Thamsten (U. Fluminense, Brazil) |
Local null controllability of a class of non-Newtonian incompressible viscous fluids
Abstract. Slides. youtube link |
| October 27 Talk 2 |
Jeffrey Park (U Alaska Fairbanks,US) |
Inverse Problem for the Schrödinger Equation with Non-self-adjoint Matrix Potential
Abstract: We consider the dynamical system with boundary control for the vector Schrödinger equation on the interval with a non-self-adjoint matrix potential. For this system, we study the inverse problem of recovering the matrix potential from the dynamical Neumann-to-Dirichlet operator. We first provide a method to recover spectral data for the Schrödinger system. We then develop a strategy for solving the inverse problem using this method with other techniques of the Boundary Control method. This talk is based on joint work with Sergei Avdonin, Alexander Mikhaylov, and Victor Mikhaylov. Slides. youtube link |
| November 3 | Belhassen Dehman (Fac. des Sciences de Tunis, Tunisia) |
Controllability of the Wave Equation on a rough compact manifold.
Abstract: The property of controllability for the wave equation has been intensively studied, mainly in a smooth framework ( smooth metric and smooth domain ). In this lecture, I will present some results on observability/control for the wave equation with rough coefficients. More precisely, we prove that the property of exact internal or boundary controllability for a wave equation with smooth coefficients is stable with respect to Lipschitz perturbations of the metric. We also consider the case of a C^1 metric ( the hamiltonian field is only continuous) and we prove the propagation up to the boundary of semi-classical measures support. The generalized Geometric Control Condition is then sufficient for exact control. This talk comes from joint works with J. Le Rousseau (Univ. Paris 13) and N. Burq (Univ. Paris Sud). Slides. youtube link |
| November 10 Talk 1 |
Kevin Le Balc'h (U Bordeaux, France) |
Exponential bounds for gradient of solutions to linear elliptic and parabolic equations.
Abstract: In this talk, I begin by introducing the Landis conjecture on exponential decay of solutions to elliptic equations. I recall the (ongoing) story of this conjecture and its link with sharp observability estimates for solutions to elliptic and parabolic equations. Motivated by "a dual version of the Landis conjecture", I present new exponential bounds for gradient of solutions to elliptic and parabolic equations. Slides. youtube link |
| November 10 Talk 2 |
Jon Asier Barcena-Petisco (U Autonoma Madrid, Spain) |
Averaged dynamics and control for heat equations with random diffusion
Abstract: In this talk we deal with the averaged dynamics for heat equations in the degenerate case where the diffusivity coefficient, assumed to be constant, is allowed to take the null value. First we prove that the averaged dynamics is analytic. This allows to show that, most often, the averaged dynamics enjoys the property of unique continuation and is approximately controllable. We then determine if the averaged dynamics is actually null controllable or not depending on how the density of averaging behaves when the diffusivity vanishes. In the critical density threshold the dynamics of the average is similar to the 1/2-fractional Laplacian, which is well-known to be critical in the context of the controllability of fractional diffusion processes. Null controllability then fails (resp. holds) when the density weights more (resp. less) in the null diffusivity regime than in this critical regime. This talk is based on joint work with Enrique Zuazua. Slides. youtube link |
| November 17 | Suzanne Lenhart (U. Tennessee, US) |
Optimal control for management of aquatic population models
Abstract: Optimal control techniques of ordinary and partial differential equations will be introduced to consider management strategies for two different aquatic populations. In the first example, managing invasive species in rivers can be assisted by adjustment of flow rates. Control of a flow rate in a partial differential equation model for a population in a river will be used to keep the population from moving upstream. The second example represents a food chain on the Turkish coast of the Black Sea. Using data from the anchovy landings in Turkey, optimal control of the harvesting rate of the anchovy population in a system of three ordinary differential equations (anchovy, jellyfish and zooplankton) will give management strategies. Slides. youtube link |
| November 24 Talk 1 |
Cristina Urbani (U. Roma Tor Vergata, Italia) |
A constructive algorithm for building mixing coupling potentials.
Application to bilinear control. Abstract. Slides. youtube link |
| November 24 Talk 2 |
Wencel Valega Mackenzie (U. Tennessee Knoxville, US) |
Resource Allocation in an Open Ecosystem
Abstract: In this talk, we propose a reaction-diffusion population model to study the effect of resource allocation in an ecosystem where resources are allowed to have their own dynamics in space and time. We also formulate and solve an optimal control problem applied to the resource allocation model where the inflow of resources is the control. The goal is to maximize the abundance of the population while minimizing the cost of inflow resource allocation. Our model can capture habitat heterogeneity to represent changes in the population instead of assuming the resource level remains homogeneous in the habitat. Some numerical simulations will be shown to illustrate the dynamics of the model. Slides. youtube link |
| December 1 | Ozkan Ozer (Western Kentucky U, US) |
Introduction of Novel PDE Models of Certain Smart Material Systems
and Diving into Related Controllability Issues Abstract: In this talk, novel PDE models for single-layer and multi-layer smart material beam systems will be introduced. These models mainly couple the longitudinal and/or transverse vibrations of layers with the electro-magnetism due to Maxwell's equations and/or thermal effects. Recent results on the exact boundary observability and controllability, stabilizability will be discussed and certain mathematical hurdles will be addressed. Even though some of these PDE models are known to be exactly observable, their approximations by the Finite-Element and Finite-Difference methods are not able to mimic this behavior with respect to the discretization parameter. Recent results on the application of a filtering technique and the issues due to the non-compact coupling between the system equations and different wave speeds through the layers will be discussed. Finally, if the time allows, recently published Wolfram's Demonstration Projects will be shown briefly and related future directions will be addressed. Slides. youtube link |
|
December 8
Talk 1 |
Jorge Zavaleta (UNAM, México) |
Radial basis function methods with hybrid kernels applied to solve control problems.
Radial basis functions (RBFs) methods have been widely applied to several fields in science and engineering in recent years. These methods are well known for attaining an exponential rate of convergence for some kernels and are flexible in dealing with complex boundaries in several dimensions. Hybrid kernels presented by Mishra et al. (2018) have, among all the available ones used in RBFs methods, the advantage of simultaneously maintaining a good condition number of the Gram matrices while preserving the exponential rate of convergence for the error. Also, they have been successfully applied to obtain the numerical solution of stationary and evolutionary partial differential equations using radial basis-finite differences (RBF-FD) (Mishra et al. 2019). Although the numerical stability of these methods has been studied, there are still theoretical and practical aspects to explain. In this talk, we present an overview of radial basis function methods with hybrid kernels and how they are applied to solve control problems numerically. We will show some recent results which have been obtained for solving distributed optimal control problems and null controllability of the Stokes equation via local RBF methods. Slides. youtube link |
| December 8 Talk 2 |
Lucas Machado (IFCE, Brazil) |
Some control results for Stokes equations with memory.
Stokes equations have been studied since many years and its understanding is very relevant from the mathe- matical and physical viewpoint. In this talk, we will consider the Stokes equations in the presence of an integro- differential term (integral in time and differential in space) called memory term. We will study the boundary null controllability problem (to steer the flow to the rest at an arbitrarily small time) for the Stokes equations with memory in the two and three dimensional cases. Precisely, we will construct explicitly initial conditions such that the null controllability does not hold even if the controls act on the whole boundary. Moreover, we also prove that this negative result holds for distributed controls. Finally, we will present some issues which remain open. Joint work with Enrique Fernández-Cara (University of Sevilla) and Diego A. Souza (University of Sevilla). Slides. youtube link |
| December 15 | Julie Valein (U Lorraine, France) |
Some results about the stability and the controllability of the KdV equation
In this talk, I present some recent results about the Korteweg-de Vries equation obtained with Lucie Baudouin (LAAS, Toulouse), Eduardo Cerpa (Pontificia Univ. Catolica de Chile) and Emmanuelle Crépeau (Univ. Grenoble Alpes). First, we show the robustness of the exponential stability of the KdV equation with respect to the delay in the boundary or the internal feedbacks, and we show that the behavior is not the same in the two situations. Then we study the boundary controllability of the KdV equation on a tree network. Slides. youtube link |
| January 7 Talk 1 |
Kuntal Bhandari (U. Toulouse, France) |
Boundary controllability of some 1-D coupled parabolic systems with Kirchhoff condition.
Abstract: In this presentation, we talk about the 1-D boundary controllability results of some 2x2 parabolic systems with both the interior and boundary couplings: the interior coupling is chosen to be linear while the boundary one is considered by means of a Kirchhoff condition at one end of the domain (0,1). The control is exerted on one of the two state components through the Dirichlet boundary condition at the other end of (0,1). In particular, we show that the controllability properties change depending on which component of the system the control is being applied. Regarding this, we point out that the choices of interior coupling coefficient and the Kirchhoff parameter play a crucial role to deduce the positive or negative controllability results. To this end, we also prescribe controllability/ non-controllability results of some 3x3 coupled systems also with Kirchhoff condition and only one boundary control. Slides. youtube link |
| January 7 Talk 2 |
Rogelio Ortigosa (Cartagena, Spain) |
Computational design and optimization of electrode meso-arquitecture for shape morphing dielectric elastomers.
Abstract: In this talk we introduce a novel computational framework for the in silico analysis and optimisation of the electrode meso-arquitecture of shape morphing Dielectric Elastomers (DEs). This contribution is deeply inspired in its conception by the work by Clarke (Clarke Lab in Harvard), who proposed a novel technology based on a layer-by-layer fabrication of elastomers sheets and electrodes to generate variable strain along the thickness with the aim of attaining a morphology or curvature changes that conventional electrode layouts are far from accomplishing. Based on this work, we explore the design of shape morphing DEs from a numerical standpoint, showcasing the convenience of topology optimisation as an extremely useful assistance tool to experienced researchers for the design of new DE devices characterised by non-intuitive electrode layouts outperforming conventional DE designs. From the numerical standpoint, the main ingredients and novelties of this work are: (i) Consideration of the phase-field method for the implicit definition of the electrodes placed at surface regions, which entails the definition of surface-restricted phase-field functions; (ii) Extension of the surface-restricted phase-field functions to the volume of the DE in order to embed the effect of the presence or absence of electrodes within the Helmholtz's energy functional of the DE; (iii) Original energy interpolation scheme of the Helmholtz's energy functional where only the electromechanical contribution is affected by the extended phase-field function; (iv) Consideration of Allen-Cahn type evolution laws for the surface-restricted phase-field functions, adapted to the current multiphysics setting; (v) A series of numerical examples are included in order to assess the applicability of the proposed methodology. Slides. youtube link |
| January 14 | Nicolas Burq (U Paris Sud, France) |
Propagation of smallness and control for heat equations.
Abstract: In this talk I will present some results on the propagation of smallness properties for solutions to heat equations. I will consider spectral projector estimates for the Laplace operator with Dirichlet or Neumann boundary conditions on a Riemanian manifold with or without boundary and on $R^d$. I will show that using as a black box the new approach for the propagation of smallness from Logunov-Malinnikova allows to extend the spectral projector type estimates from Jerison-Lebeau from localisation on open set to localisation on arbitrary sets of non zero Lebesgue measure; I will actually go beyond and consider sets of non vanishing $d- \delta$, ($ \delta >0$ small enough) Hausdorf measure. I will show that these new spectral projector estimates allow to extend the Logunov-Malinnikova's propagation of smallness results to solutions to heat equations. Finally I will apply these results to the null controlability of heat equations with controls localised on sets of positive Lebesgue measure. A main novelty here with respect to previous results is that we can drop previous the constant coefficient assumptions of the Laplace operator (or analyticity assumption) and deal with Lipschitz coefficients. Another important novelty is that we get the first (non one dimensional) exact controlability results with controls supported on zero measure sets and at discrete times. This is a joint work with I. Moyano (université de Nice). Slides. youtube link |
| January 21 Talk 1 |
Denilson Menezes (U.F. Fluminense, Brazil) |
On equilibria for generalized Boussinesq fluid-chemical models with multiplicative controls
Abstract: We investigate equilibria for multi-objective optimal control problems in a model of fluid-chemical interactions. The action of the controls occurs multiplicatively, a pertinent assumption for certain practical circumstances, e.g., the study of ocean pollution control. For a single agent, we provide a characterization of the Pareto front in terms of a suitable class of minimization problems, each of which being equivalent to solving an optimality system. In the multi-agent competitive setting, each agent seeks to minimize her performance criteria to attain Pareto optimality, and we investigate Nash equilibria in this context. We derive and analyze the resulting optimality system in the latter framework. Slides. youtube link |
| January 21 Talk 2 |
Mihai Nechita (INRIA Paris) |
Unique continuation problems and stabilised finite element methods
Abstract: We consider the unique continuation problem for elliptic PDEs with data given in an interior subset of the domain. This is an ill-posed problem that arises often in inverse problems and control theory. We focus on the Helmholtz and the convection-diffusion equations and present first conditional stability estimates that are explicit in the physical parameters. Under a geometric convexity assumption, we show that for the Helmholtz equation the stability constants grow at most linearly in the wave number. We then discuss a finite element method based on a discretise-then-regularise approach. We cast the problem into PDE-constrained optimisation with discrete regularisation inspired from stabilised FEM. Our focus is on the interior penalty stabilisation. Convergence rates are obtained by applying the continuum stability estimates to the approximation error and controlling the residual through stabilisation. For convection-dominated problems, we obtain sharper weighted error estimates along the characteristics of the convective field through the data region. The results are illustrated by numerical examples. This is joint work with Erik Burman and Lauri Oksanen. Slides. youtube link |
| January 28 | Lauri Oksanen (University College London) |
Spacetime finite element methods for control problems subject to the
wave equation
Abstract: We consider the null controllability problem for the wave equation, and analyse a stabilized finite element method formulated on a global, unstructured spacetime mesh. We prove error estimates for the control function given by the computational method. The proofs are based on the regularity properties of the control function given by the Hilbert Uniqueness Method, together with the stability properties of the numerical scheme. The talk is based on joint work with Erik Burman, Ali Feizmohammadi and Arnaud Münch. Slides. youtube link |
| February 4 Talk 1 |
Cristobal Merono (Madrid, Spain) |
The fixed angle scattering problem with a first order perturbation
In this talk we present recent results on the inverse scattering problem for the Schrödinger equation that consists in determining a magnetic field and electric potential from scattering measurements corresponding to finitely many plane waves. The main result shows that the coefficients are uniquely determined by 2n measurements up to a natural gauge. We also show that one can recover the full first order term for a related equation having no gauge invariance, and that it is possible to reduce the number of measurements if the coefficients have certain symmetries. This work extends the fixed angle scattering results of Rakesh and M. Salo to Hamiltonians with first order perturbations, and it is based on wave equation methods and Carleman estimates. Slides. youtube link |
| February 4 Talk 2 |
Shengquan Xiang (EPFL, Switzerland) |
Quantitative rapid and finite time stabilization of the heat equation
The finite time stabilization of the 1D heat equation was proved by Coron-Nguyen (2015) via backstepping, while the multidimensional cases remained open. Inspired by Coron-Trélat's Lyapunov approach (2004) we construct explicit stationary feedback laws that quantitatively rapidly stabilize the heat equation, where the spectral inequality of Lebeau-Robbiano type (1995) is naturally adapted. Next we construct explicit controls leading to the null controllability sharing optimal costs $e^{C/T}$, and further prove the finite time stabilization. We also talk about the stabilization of Navier-Stokes equations. Slides. youtube link |
| February 11 | Rafael Vazquez (U Sevilla, Spain) |
Backstepping for PDEs: fundamentals and some recent results
In this talk, I will start by reviewing the backstepping method for boundary control of Partial Differential Equations (PDEs), its main ingredients (selection of a judicious target system, use of an invertible integral transformation, solution of the corresponding kernel equations) and in particular its usefulness for coupled parabolic and hyperbolic systems. The rest of the talk is then devoted to some recent results on a few topics: the Rijke tube, modelled by coupled hyperbolic PDEs and ODEs, where some preliminary experimental results are available; extensions to n-dimensional parabolic systems, which present challenges for backstepping since it is not clear how to pose the system transformation; and coupled parabolic-hyperbolic systems, for which few results are available due to the difficulty in finding the right target system and transformation. These results have been obtained in collaborations with several authors, including M. Krstic, G. A. de Andrade, J. Zang, G. Chen, and others, which will be credited during the talk. Slides. youtube link |
| February 18 Talk 1 |
Christophe Zhang (U Erlangen, Germany) |
Stabilization of controllable systems: application to the water tank
In this talk, we show how the ideas of backstepping for PDEs can be combined with the notions of system equivalence and pole-shifting to stabilize some controllable systems. This can be thought of as a variant of backstepping for internal distributed controls, which uses a Fredholm-like transformation instead of the "usual" Volterra transformation of the second kind. This strategy of proof was already used to stabilize the linearized bilinear Schrödinger equation. It can be adapted to stabilize the 1-D linear transport equation. The contrasting spectral properties of these systems lead to very different technical developments. We will focus in particular on the stabilization of a 1-D water tank. It can be shown, using a moments method with some sharp estimates, that the linearized systems around non-uniform steady states are controllable in Sobolev spaces (up to conservation of mass). We use this partial controllability result to construct exponentially stabilizing feedbacks for the linearized water-tank system around non-uniform steady states. This shows that the method can be adapted to more complex hyperbolic systems, despite the additional difficulties due to the coupling terms, and the conservation of mass. Slides. youtube link |
| February 18 Talk 2 |
Cyril Letrouit (ENS Paris) |
Exact controllability properties of subelliptic wave and Schrödinger equations
We present several results concerning exact controllability and observability properties of subelliptic PDEs, i.e., PDEs driven by a subelliptic Laplacian. Our first result is that subelliptic wave equations are never controllable/observable. Then, considering various families of subelliptic operators, we explain that subelliptic Schrödinger-type equations can be controllable in any time, or never controllable, or controllable only for sufficiently large time. This last part was done in collaboration with Chenmin Sun and Clotilde Fermanian Kammerer. The tools used in this presentation come from various fields: sub-Riemannian geometry, semi-classical analysis, spectral theory and non-commutative harmonic analysis. Slides. youtube link |
| February 25 | Irena Lasiecka (U Memphis, US) |
Control of a third order in time dynamics governing nonlinear acoustic waves - a view from the boundary.
Abstract. Slides. youtube link |
| March 4 Talk 1 |
Yacine Mokhtari (Besancon, France) |
Boundary stabilization of the 1-D wave equation on non-cylindrical domains
Boundary stabilization of the 1-D wave equation on non-cylindrical domains (or domains with moving boundaries) is discussed. By using a time-varying feedback law acting on one side of the boundary, we provide a necessary and sufficient condition for the stabilization at any desired decay rate. Furthermore, the influence of the boundary shape on the decay rate is clarified. Some particular examples are discussed. Slides. youtube link |
| March 4 Talk 2 |
Thomas Ian Ashley (Sevilla, Spain) |
New methods and results for the optimisation of solar power tower plants
Research into renewable energy sources has continued to increase in recent years, and in particular the optimisation and application of solar energy systems. In this work, the authors consider multiple operations research models and develop bespoke algorithms to maximise the efficiency of various subsystems of a solar power tower plant. Results are presented using real-world data and future research topics are discussed. Slides. youtube link |
| March 11 | Fredi Tröltzsch (TU Berlin, Germany) |
On Optimal Control Problems with Controls Appearing Nonlinearly in an Elliptic State Equation
An optimal control problem for a semilinear elliptic equation is discussed, where the control appears nonlinearly in the state equation but is not included in the objective functional. This feature needs a special treatment that is addressed in this talk. We prove the existence of optimal controls by a measurable selection technique and present two types of second-order sufficient optimality conditions. A first theorem invokes a well-known assumption on the set of zeros of the switching function. A second relies on coercivity of the second derivative of the reduced objective functional. The theory is complemented by associated examples. Moreover, it is applied to the convergence of optimal state functions under a finite element discretization of the control problem. This is a joint work with Eduardo Casas (Santander). Slides. youtube link |
| March 18 Talk 1 |
Constantinos Kitsos (Toulouse, France) |
Output feedback control of an under-actuated and under-observed cascade system of linear Korteweg-de Vries equations.
In this talk we will present the stabilization of a cascade system of n linear Korteweg-de Vries equations in a bounded interval. An output feedback control is placed at the left endpoint of the last equation, while the output involves only the solution to the first equation. The boundary control problems investigated include two cases: a classical control on the Dirichlet boundary condition and a less standard one on its second-order derivative. The feedback control law utilizes the estimated solutions of an observer system and the output feedback control leads to stabilization for any n for the first boundary conditions case and for n=2 for the second one. Finally, we will discuss observer and control design problems for systems of PDEs with more general couplings, when we have fewer controls and observations than the number of states. This talk is based on joint work with Eduardo Cerpa, Gildas Besançon, and Christophe Prieur. Slides. youtube link |
| March 18 Talk 2 |
Exequiel Mallea Zepeda (Tarapaca, Chile) |
Optimal control problems related to chemo-repulsion systems.
In this talk we present bilinear optimal control problems related to chemo-repulsion systems with linear and superlinear production terms in the 2D case and linear in the 3D case. We establish results on existence of global optimal solutions and derive the respective optimality systems, based on a result of the existence of Lagrange multipliers in Banach spaces. Finally, we analyze the main differences (and difficulties) between the 2D and 3D cases. youtube link |
| March 25 | Assia Benabdallah (Marseille, France) |
Control of parabolic equations.
Abstract. Slides. |
| April 8 Talk 1 |
Armand Koenig (Paris, France) |
Null-controllability of parabolic-transport systems.
Abstract: We consider the null-controllabillity problem for systems of equations coupling parabolic equations and transport equations. This problem requires combining arguments adapted for parabolic equations and arguments suitable for transport equations, which are of different nature. We manage to do it for 1 dimensional, periodic boundary conditions, constant coefficients systems. Results for several particular cases of such equations were already known in the litterature, and we get this way close variants of these theorems. In this talk, we will present the ideas of our method to tackle these systems. Slides. youtube link |
| April 8 Talk 2 |
Thibault Liard (Nantes, France) |
Boundary sliding mode control of hyperbolic systems
Abstract. Slides. youtube link |
| April 15 | Daniel Faraco (UA Madrid, Spain) |
Homogenization and Inverse Problems.
Abstract: I will review some conditional stability results and recovery algorithms in various inverse problems with irregular coeficients. The arguments use the quasiconformal mappings and a connection with the nonelliptic time dependent Schrödinger equation. Then I will discuss in detail how G-convergence can be utilized to create instabilities in inverse problems. The latter is a work with Y. Kurylev and A. Ruiz. If time allows, I will sketch part of a program with Guijarro, Kurylev and Ruiz to homogenize elliptic equation in paralellizable manifolds. Slides. youtube link |
| April 22 Talk 1 |
Swann Marx (Nantes, France) |
One-dimensional wave equation with set-valued damping: well-posedness, asymptotic stability, and decay rates.
Abstract: In this presentation, the focus will be on a one-dimensional wave equation with a set-valued boundary damping. This (general) framework allows to consider nonlinear dampings such as saturations (i.e. nonlinearities modeling amplitude constraints) or dry dampings (a nonlinearity given by a sign function). The approach that will be presented consists in transforming the one-dimensional wave equation as a scalar discrete nonlinear differential inclusion. It is a general approach that could be applied on more general systems. It allows to obtain several results: a necessary and sufficient condition for the well-posedness; asymptotic stability in L^p type functional spaces; optimality of decay rates. The well-posedness result and some asymptotic stability results will be presented during the presentation. It is a joint work with Yacine Chitour and Guilherme Mazanti. Slides. youtube link |
| April 22 Talk 2 |
Guilherme Mazanti (L2S, Paris) |
Asymptotic behavior of one-dimensional wave equations with set-valued boundary damping.
Slides. youtube link |
| April 29 | Dante Kalise (School of Mathematical Sciences, University of Nottingham) |
High-dimensional Hamilton-Jacobi PDEs: Approximation, Representation, and Learning.
Abstract: Hamilton-Jacobi PDEs are a central object in optimal control and differential games, enabling the computation of robust controls in feedback form. High-dimensional HJ PDEs naturally arise in the feedback synthesis for high-dimensional control systems, and their numerical solution must be sought outside the framework provided by standard grid-based discretizations. In this talk, I will discuss the construction novel computational methods for approximating high-dimensional HJ PDEs. In the first part of the talk, I will present a numerical method based on tensor decompositions. Such a compressed representation of the value function has a complexity that scales linearly with respect to the dimension of the control system, allowing the solution of control problems over very high-dimensional states. In the second part of the talk, I will discuss the construction of a class of causality-free, data-driven methods which circumvent the numerical solution of the HJ PDE. I will address the generation of a synthetic dataset based on the use of representation formulas (such as Lax-Hopf or Pontryagin's Maximum Principle), which is then fed into a high-dimensional sparse polynomial model for training. The use of representation formulas providing gradient information is fundamental to increase the data efficiency of the method. I will present applications in control of nonlinear PDEs and agent-based models. Slides. youtube link |
| May 6 Talk 1 |
Lina Guan (Grenoble, France) |
Optimal Observer-based Output Feedback Controller for Traffic Congestion with Bottleneck.
Abstract: This paper designs an optimal observer-based output feedback control for traffic breakdown to dissolve traffic congestion using the backstepping method and optimization. The linearized Aw-Rascle-Zhang model is used to represent the congested traffic dynamics resulting from traffic breakdown. Based on the factors leading to traffic breakdown, we take into account the boundary conditions consisting of a boundary with a constant density and a speed drop at the upstream inlet of a bottleneck, and a boundary with a disturbance of inflow (high traffic demand) at the inlet of the road segment under consideration. To dissolute traffic congestion, a dynamic feedback controller is designed at the upstream boundary. By using the backstepping approach, an observer-based output feedback controller is computed to guarantee the integral input-to-state stability of the closed-loop system. By establishing an optimization problem and solving it, the optimal value of the considered class controller is obtained. The performance of the output feedback controller is also validated by numerical simulations. Slides. youtube link |
| May 6 Talk 2 |
Marcu-Antone Orsoni (Bordeaux, France) |
On the reachable space of the heat equation.
Abstract: It is well-known that the heat equation is not exactly controllable from the boundary because of the smoothing effect of its kernel. One can then ask which are the states that we can reach at a given time. After an overview of the previous results since the pioneering work of Fattorini and Russell in 1971, we will give a definitive description of the reachable set of the one-dimensional heat equation on a segment as the Bergman space of a certain square. This result involves complex and harmonic analysis tools as a separation of singularities theorem for the Bergman space. Finally, we will discuss the case of the Hermite heat equation. This talk is based on joint works with Andreas Hartmann. Slides. youtube link |
| May 13 | Alessandro Alla (PUC, Rio, Brazil) |
HJB-RBF based approach for the control of PDEs
Abstract: Semi-Lagranian schemes for discretization of the dynamic programming principle are based on a time discretization projected on a state-space grid. The use of a structured grid makes this approach not feasible for high-dimensional problems due to the curse of dimensionality. Here, we present a new approach for infinite horizon optimal control problems where the value function is computed using Radial Basis Functions (RBF) and Shepard’s moving least squares approximation method on scattered grids. We propose a new method to generate a scattered mesh driven by the dynamics and the selection of the shape parameter in the RBF using an optimization routine. Numerical tests for high dimensional problems will show the effectiveness of the proposed method. Joint work with H. Oliveira (PUC-Rio, Brazil) and G. Santin (FBK, Italy). Slides. youtube link |
| May 20 Talk 1 |
Imene Djebour (U. Lorraine, France) |
Local null controllability of a fluid-rigid body interaction problem with Navier slip boundary conditions
Abstract: The aim of this work is to show the local null controllability of a fluid-solid interaction system by using a distributed control located in the fluid. The fluid is modeled by the incompressible Navier-Stokes system with Navier slip boundary conditions and the rigid body is governed by the Newton laws. Our main result yields that we can drive the velocities of the fluid and of the structure to 0 and we can control exactly the position of the rigid body. One important ingredient consists in a new Carleman estimate for a linear fluid-rigid body system with Navier boundary conditions. This work is done without imposing any geometrical conditions on the rigid body. Slides. youtube link |
| May 20 Talk 2 |
Esteban Hernández (Universidad Técnica Federico Santa María Valparaíso, Chile) |
Rapid stabilization of a unstable heat equation under boundary disturbance
Abstract: In this presentation we address the problem of rapid stabilization of a one dimensional unstable heat equation under the action of a unknown boundary disturbance. Combining the backstepping method and the multivalued operator sign, we design a boundary feedback law which exponentially stabilizes the system, in the L2 norm. Moreover, the rate can be fix arbitrarily large. The existence of solutions to the closed-loop system it is obtained by using the theory of maximal monotone operators. Numerical simulations are performed in order to illustrate our results. It is a joint work with Patricio Guzman, UTFSM, Valparaíso Chile. Slides. youtube link |
| May 27 | Delphine Bresch-Pietri (Mines Paristech, Paris) |
Control of linear and nonlinear systems subject to a random input delay
Abstract: This talk will study the stabilization problem of Ordinary Differential Equations subject to a random input delay, modeled as a Markov process with a finite number of states. We propose to robustly compensate for the random delay with a constant-time horizon prediction based-controller. Recasting the dynamics as a cascade of hyperbolic Partial Differential Equations into an ODE, we prove well-posedness of the closed-loop system and provide sufficient conditions for its mean-square stability. These conditions bear on the range of the delay values, which has to be sufficiently narrow, and the prediction horizon which should stay sufficiently close to the potential delay values. We will illustrate the numerical relevance of these conditions on linear and nonlinear systems. Finally, we will draw methodological perspectives for the analysis of stochastic cascades of ODE-PDE systems. Slides. youtube link |
| June 3 Talk 1 |
Stephen Guffey (U. Memphis, US) |
Local Null Controllability for a Chemotactic Model for Bacterial Infection in a Chronic Wound
In this talk we study a coupled ODE-PDE system as a model for a bacterial infection in a chronic wound. The model consists of three parabolic-type equations with an ODE. Coupling comes by way of nonlinear source/decay terms as well as chemotactic coupling. We first consider the well-posedness of the model. After which, we consider the local controllability of the model to a desired state in which the invasive bacteria are driven to extinction. In doing so, we need to take advantage of the available Carleman inequalities to show the observability inequality associated to our adjoint system. Slides. youtube link |
| June 3 Talk 2 |
Jehan Alswaihli (U. Reading, UK) |
Iteration of inverse problems and data assimilation techniques for neural field equations.
Data assimilation is concerned with state estimation in dynamical systems. Meanwhile, the reconstruction of unknown parts of some dynamical system such as structural functions or connectivity is a basic task of inverse problems, medical imaging and nondestructive testing. As an example, we study the re- construction of the neural connectivity kernel within a neural field given the full dynamical evolution. Then, we formulate an iterative data assimilation inversion method. Where the activity fields of some neural tissue is recon- structed from non-local measurements and the kernel is reconstructed given the reconstruction of the activity. This approach is iterated in the sense that the first guess for the state reconstruction can be improved based on the kernel reconstruction of step two. youtube link |
| June 10 | Larisa Beilina (Chalmers, Sweden) |
Finite element analysis of an inverse problem for Maxwell's equations with application to microwave thermometry
We will present an adaptive finite element method for solution of an inverse problem for Maxwell's equations in conductive media where the goal is to determine the complex dielectric permittivity function. We derive a posteriori error estimates in the functional to be minimized and in the regularized solution to this functional, and formulate corresponding adaptive algorithms. Balancing principle for optimal choice of the regularization parameter will be presented. Finally, numerical experiments will show the efficiency of a posteriori estimates applied to data measured in microwave thermometry for real-time monitoring of tumour during microwave hyperthermia process. youtube link |
| June 17 Talk 1 |
Hugo Parada (U Grenoble) |
Global Well-posedness of KdV equation on a Star Shaped Network and an application to saturated stabilization
In this talk we deal with the global well-posedness and stability of the nonlinear and linear Korteweg-de Vries (KdV) equation on a finite star-shaped network by acting with saturated controls. We obtain the global well-posedness by using the a Sharp Kato smoothing property for the linear case and then using somes estimates and a fixed point argument we deal with the nonlinear system. Finally we obtain the semi-global exponential stability of two different kinds of saturation using a contradiction argument to prove appropriated observability inequalities. youtube link |
| June 17 Talk 2 |
Luca Saluzzi (GSSI, Italy) |
A matrix oriented HJB-POD method for the control of PDEs on a tree structure
The classical Dynamic Programming (DP) approach to optimal control problems is based on the characterization of the value function as the unique viscosity solution of a Hamilton-Jacobi-Bellman (HJB) equation. We will discuss a new approach for finite horizon optimal control problems where we compute the value function on a tree structure constructed directly by the time discrete dynamics and we do not use a space triangulation to solve the HJB equation. We will also apply a novel matrix-oriented reduction process (Two-sided POD-DEIM) leading to an effective, structure aware low order approximation of the original problem. Furthermore, we provide an error estimate which guarantees the convergence of the proposed method. Finally, we show the efficiency of the method through numerical tests on linear and nonlinear PDEs. This is a joint work with Maurizio Falcone (La Sapienza, Roma) and Gerhard Kirsten (Università di Bologna). Slides. youtube link |
| June 24 | Frédéric Marbach (Rennes, France) |
Expansions for nonlinear systems, error estimates and convergence issues
This talk is about solving time-dependent ODEs, related with control theory. We present methods to compute approximations of the final state of the system. In particular, we recall the classical Chen-Fliess expansion and compare it with the lesser used Magnus expansion. We also introduce a new expansion, specifically designed for applications to local control results, which yields approximations of the final state at any order in the size of the control. Slides. youtube link |
| July 1 Talk 1 |
Jose Henrique Rodrigues (U. Memphis, US) |
On the well-posedness and stabilization of a nonlinear structural-acoustic interaction problem
In this talk, we are going to discuss the well-posedness and the topics of stabilization of a nonlinear structural-acoustic system. To be precise, the model consists on the interactions of acoustic waves in a 3D bounded domain (also called medium or chamber) with the vibrations of some portion of the boundary, also called structural wall, governed by a nonlinear plate equation. The acoustic problem is subject to boundary dissipation and Neumann boundary conditions, while the dynamics in the structural wall is given by a 2D Kirchhoff-Boussinesq equation. youtube link |
| July 1 Talk 2 |
Cristhian Montoya (U. of Dubrovnik, Croatia) |
Robust Stackelberg controllability for the Kuramoto-Sivashinsky equation
In recent works, the notion of searching for a robust control system is developed simultaneously with a strategy on hierarchic control. From a mathematical point of view, the robustness of a system is equivalent to find a saddle point because we are looking for maximizing the perturbation and simultaneously minimizing the control which stabilizes the system. In addition, a hierarchic control strategy appears on the system, namely, a Stackelberg strategy, which establishes a game between two forces (called follower and leader) into the system.The scheme shows a robust control problem for the follower control and its associated disturbance function. Afterwards, we consider a Stackelberg optimization (which is associated to the leader control) in order to deduce a controllability result for the Kuramoto-Sivashinsky equation. Slides. youtube link |
| July 8 | Franck Boyer (Toulouse, France) |
The block moment method in action
The main objective of this talk is to present a new null-controllability result for a 2D system of two coupled parabolic equations, with different diffusion coefficients, under the action of only one boundary control. We prove, in particular, that short-time controllability holds for this problem whereas it is not necessarily the case for the similar system in 1D. The proof appears to be a somehow unexpected application of the block moment method, that I will describe during the talk. Slides. youtube link |
| July 15 Talk 1 |
Rodrigo Lecaros (UTFSM, Chile) |
Stability estimate for the semi-discrete linearized Benjamin-Bona-Mahony equation
The main goal of this talk is to present a unique continuation property (UCP) for the semi-discrete linearized Benjamin-Bona-Mahony equation (BBM). This equation is a model for propagating one-dimensional, one-directional, and small-amplitude long waves in non-linear dispersive media. The proof is based on a Carleman estimate for a finite difference approximation of the Laplace operator with boundary observation. The Carleman's parameter is connected to the mesh size; despite this limitation, it is possible to obtain a UCP similar to that of the continuous case. youtube link |
| July 15 Talk 2 |
Andrew Walton Green (Washington U, St Louis, US) |
Local and Global Estimates for Holomorphic functions
I will discuss "three-sphere" inequalities for holomorphic functions where the three spheres can actually be any three sets of positive Lebesgue measure which satisfy a certain boundary separation property. We will discuss some new and old applications of such inequalities to control and observability for parabolic and hyperbolic equations. youtube link |